Introduction¶
The Large Synoptic Survey Telescope (LSST) “Stack” currently uses an implementation of [3]‘s Optimistic Pattern Matcher B (OPMb) for blind astrometric matching to a reference catalog. This has been found to have a significant failure mode in very dense stellar fields with ~1000 references per CCD. This is caused by the algorithm being too greedy and finding false astrometric matches due to the matching space no longer being sparse at these densities. Rather than fine tune parameters for this algorithm to match successfully, we generalize the [3] algorithm to work consistently over the large range of stellar densities expected in LSST. In this work we present Pessimistic Pattern Matcher B (PPMb), which operates over the full dynamic range of densities expected in LSST.
Method overview¶
Background¶
In this section we describe the modifications and generalizations we make to OPMb to create PPMb. Like OPMb, PPMb relies on matching \(N\) point pinwheel patterns between a source catalog and a catalog of astrometric reference objects. This allows the matching to account for both shifts and rotations in the WCS with some allowance for distortion or scaling. Searching for such pinwheel shapes rather than triangles allows for efficient creation of, and searching for patterns “on the fly” [3] rather than pre-computing all of the \(n (n - 1) (n - 2) / 6\) unique triangles available in a reference catalog with \(n\) elements. Instead the algorithms need only pre-compute the \(n (n - 1) / 2\) unique pairs between reference objects.
In [3] OPMb is tested only up to hundreds of reference objects in a given observation. However, in the galactic plane, using the Gaia catalog as a reference, there can be of order 5000 reference objects in single CCD with a similar or greater number of detected sources. Experience with our current OPMb implementation indicates that this results in an excessive number of false positive matches and, ultimately, poor astrometric solutions. PPMb is an attempt to address these issues.
Primary differences with respect to OPMb¶
PPMb follows a very similar algorithmic flow to that of the LSST implementation of OPMb with the following key differences:
- Matches are made to the reference catalog on the unit sphere rather than a tangent plane. As implemented in the Stack, OPMb relies on an intermediate tangent plane calculated from the mean positions of the astrometric references in RA, dec and detected sources in x, y on the CCD to compute matches. PPMb avoids this by searching for matches directly on the unit sphere of RA, dec.
- Can require that a specified number of successful pattern matches with the same shift and rotation on the sky be found before returning an affirmative match. This is useful in fields with a very high number of astrometric reference objects where matching an \(N\) point pattern at a realistic tolerance is fairly common. This allows PPMb to exclude false positive matches even for relatively loose tolerances.
- Allows for matching a pattern of \(N\) spokes from \(M\) points where \(M\) can be greater than \((N + 1)\). This allows the matcher skip over objects that may not be in the reference sample due to the astrometric reference sample, for instance, being observed in a different bandpass filter.
- Automatically estimates matching tolerances from the input data rather than requiring arbitrary tolerances to be set. Arbitrarily setting the tolerance can lead to instances of false positives or long run times as the algorithm is forced to fail on all test patterns before softening the match tolerance and trying again.
- Treats both the shift and rotation matching parameters as known upper bounds. This means that the known pointing error of the telescope can be used to set limits on the match, in contrast to our OPMb implementation which treats these as parameters which may be softened during matching.
- The maximum shift is tightened in addition to matching tolerance as the match-fit cycle of the algorithm improves. Since the Stack’s OPMb implementation uses an intermediate tangent plane calculated from the mean RA, dec and x, y positions of the references and sources, it is unable to utilize such a tightening. Tightening the maximum shift allows the code to find a match much more rapidly in later iterations of the WCS match-fit cycle.
Algorithm step-by-step¶
Overall approach¶
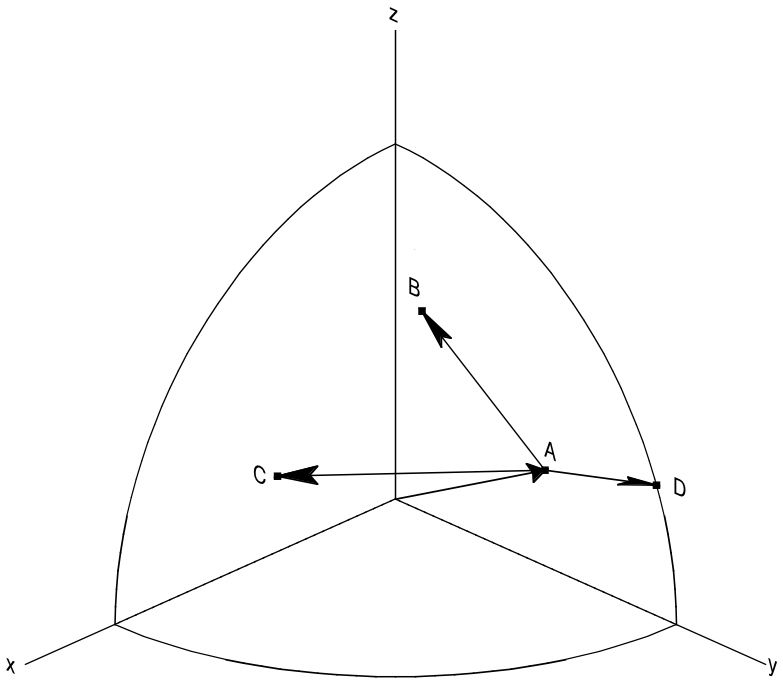
Figure 1 Illustration of an example pinwheel pattern that is searched for in the reference objects. Points A, B, C, and D are source points ordered from brightest to faintest. To find a match all lengths of the pinwheel spokes (e.g. \(|v_B - v_A|\)) and opening angles between spokes (e.g. the angle between vectors \(v_B - v_A\) and \(v_C - v_A\)) must be within tolerances \(\delta_{tol}\) and \(\delta_{ang}\) respectively. Shifts and rotations between the source and reference catalog are tested against the unit vector \(v_A\) and vector delta \(v_B - v_A\) respectively.
Both OPMb and PPMb construct “pinwheel” shapes that are used to search within the reference objects from the detected source catalog by ordering the objects in the catalog from brightest to faintest flux. The image in Figure 1 shows this pinwheel in three dimensions. The pinwheel is created by choosing the first first \(N\) brightest objects, treating the brightest of these as the pinwheel center (labeled \(A\)). The fainter If this pattern is not found in the astromtetric references then the brightest source is discarded and a new \(N\) point pinwheel is constructed starting with the second brightest object and so on until a requested number of patterns have been tested. In the current LSST implementation, the default value of \(N\) is 150.
Initialization¶
The PPMb algorithm begins by creating the data structures needed to both search for individual pattern spokes based on their distance and to compare the opening angle between different spokes. For each reference pair we pre-compute the 3-vector delta (\(v_{\Delta}=v_B - v_A\)), distance between the objects (\(|v_A - v_B|\)), and catalog IDs of the objects that make up the pair. Each of these arrays is sorted by the distance. We also create a lookup table that enables quick access to all pairs featuring a given reference object.
Shift and rotation tests¶
After selecting \(N\) sources ordered from brightest we compute the \(v_{\Delta}\) of the first two brightest points, and search for reference pairs with a distance \(|v_R|\) that have the same length to within \(\pm \delta_{tol}\) of the length of the source vector \(|v_S|\). We test each of these reference pairs from the smallest length difference \(\Delta = abs(|v_S| - |v_R|)\) to the largest, assuming that the correct pattern has nearly the same length for the source and length deltas.
These candidate pairs are then tested by first selecting one of the two reference points that make up the pair as the center of the pinwheel. By taking the dot product of the two unit-vectors representing the source center and candidate reference center, we can quickly check if the implied pointing shift is within the maximum allowed. If the shift is too large we then check against the other point in the reference pair. If both fail then we move to the reference pair with the next smallest \(\Delta\) and repeat.
Once a candidate reference pair and reference center are found to within the distance and shift tolerance, we compute the rotation matrix to align the source and reference centers. We apply this rotation to the source 3-vector rotating it into the reference frame. We then compute the dot-product of this 3-vector with the candidate reference 3-vector delta to compute the implied rotation of this candidate pair. If it is greater than our set maximum we continue to the next candidate reference pair.
Pattern construction¶
Assuming the reference candidate for the two brightest objects in the source pinwheel satisfies all of the previous tests we begin to create the remaining spokes of our \(N\) point pinwheel, in order of decreasing brightness. We first pare down the number of reference pairs we need to search by using the ID lookup table to select only reference pairs that contain our candidate reference center. This speeds up the next stages of the search significantly. We search for the reference spokes that match within tolerance in the same way as the previous step.
Once we have the candidates for this source spoke we need only test that the opening angle between this spoke and the initial spoke are within tolerance to the angle formed by the candidate reference objects. We make the assumption here that the separations between any point in the source or reference objects are small enough that we can assume simple 2D relations and that our dot and cross-products of difference vectors are within the plan of the sky.
We employ two separate but related tests to check that the opening angle between source pattern spoke we are testing and the spoke created by the two brightest source objects in the pattern is within tolerance of the corresponding reference angle.
We start by establishing the appropriate tolerance, \(\delta_{ang}\). Given the \(L\), the length of the source spoke being tested, we define:
This sets tolerance allowed between the reference and source pattens when comparing opening angle between two spokes. This avoids the user having to specify an arbitrary tolerance when configuring the algorithm. We set a limit that this angle be less than \(0.0447\) radians. This is set such that \(\cos(\delta_{ang}) \sim 1\) to within 0.1%. This allows us to use the small angle sine and cosine expansions in the coming comparisons. The tolerance assumes that \(L \gg \delta_{tol}\). When this is not the case, we instead set the opening angle tolerance to the value \(0.0447\). One can see examples of the angle under test in Figure 1 as the opening angle between the vectors \(v_B - v_A\) and \(v_C - v_A\): we ensure tha that the angles between these vectors as measured in the source and candidate reference patterns differ by no more than \(delta_{angle}\).
To test the opening angle against the current tolerance for this spoke, we compute the normalized dot-product between our source spoke to the first source spoke and do the same with the candidate reference spokes. We then test the difference of these two cosines:
If we assume that at most \(\theta_{src} = \theta_{ref} \pm \delta_{ang}\) and Taylor expand for small \(\delta_{ang}\) then we can write our test as
To avoid an expensive calculation of \(\sin\theta_{ref},\) square the above, giving:
This test on the difference in cosines is insufficient to demonstrate that the two opening angles are the same within tolerance because it does not test chirality and because of degeneracies due to the periodic nature of the functions.
To completely test that the angles are within tolerance we also need to test the sine of the angles. Here, we compute the normalized cross-product between the two source spokes and likewise the reference spokes. This produces vectors with lengths \(\sin(\theta_{src})\) and \(\sin(\theta_{ref})\) respectively. These vectors can be dotted into the center point of the the respective patterns they are derived from giving the value of the sine. It should be noted here that the value is approximate as the vectors are likely slightly misaligned to that of center points, artificially decreasing the amplitude of the sine. However, on the scale of a a CCD, the vectors we are comparing are within the plane of the sky and thus the comparison holds.
If we again Taylor expand for small angle differences the comparison becomes
These tests in tandem assure us the opening angles are the same between the source and reference spokes and that they rotate in the same direction. The tests are robust for all values the opening angles for both the reference and source patterns.
Intermediate verification¶
Once we have constructed the complete pinwheel pattern of the requested complexity, we test that the shift and rotation implied by the first spoke in each of the source and reference pinwheels can align the reference and source patterns on top of each other such that the distances between the source and reference points that make up the pinwheels are all within the matching tolerance. If this condition is satisfied we then fit a rotation matrix using the \(N\) matched points that transforms source objects into the reference frame. To permit for some distortion in the final verification process, this matrix is allowed to be non-unitary.
Pessimism of the algorithm¶
Up until this point PPMb has followed roughly the same algorithm as OPMb, although it uses vectors in 3-space on the unit-sphere instead of on the a focal plane. However, having successfully completed intermediate verification, the approaches diverge.
A series of test points are generated by computing the mean 3-vector of the source sample and creating six points by replacing each Cartesian coordinate in turn first by the minimum and then the maximum of the sample (thus \([x_{min}, \overline{y}, \overline{z}]\), \([y_{max}, \overline{y}, \overline{z}]\), etc).
Upon finding a candidate reference pattern we rotate the test points from the source into the reference frame using the rotation produced by intermediate verification. We then store these rotated test points and continue our search, starting another \(N\) point source pinwheel pattern. Once we find more patterns that pass intermediate verification, we rotate the 6 points again and compare their rotated positions to previous shifts and rotations that have been matched. If a user-specified number of previous shifts and rotations move the test points to within the \(\delta_{tol}\) length tolerance then we can proceed to the final verify step.
In tests we have shown that finding three such matches reduces the false positive rate for dense stellar fields significantly even for large values of \(\delta\). We also set a threshold for using this pessimistic mode requiring that both the number of reference objects and source objects exceeds the total number of source patterns to test before softening tolerances. This assures us that there are enough objects to have the desired number of matching patterns.
Final verification¶
Finally, after finding a suitable shift and rotation matrix we apply it and its inverse to the source object and reference object positions respectively. We construct searchable k-d trees using the spatial algorithm in SciPy. This is done for both the source and reference objects in their respective frames for fast nearest-neighbor look up. After matching the rotated source and rotated reference objects with the k-d tree we construct a “handshake” match. This matching refers to having both the sources matched into the reference frame and the reference matched into the source frame agree on the match in order to consider it valid. This cuts down on false positives in dense fields. After trimming the matched source and references to the maximum match distance \(\delta_{tol}\), we test that the number of remaining matches is greater than the minimum specified. Once this criteria is satisfied we return the matched source and reference catalog.
Softening tolerances¶
PPMb has two main tolerances which can be softened as subsequent attempts are made to match the source data to the reference catalog. These are the maximum match distance \(\delta_{tol}\) and the number of spokes which can fail to find a proper match before moving on to the next center point. We soften the match distance by doubling it after the number of source patterns requested has failed. We also independently add 1 to the number of spokes we attempt to test before exiting. We still require the same \(N\) point complexity of the pattern but we can test a total number of \(N-M-2\) spokes before exiting. These two softenings allow the algorithm enough flexibility to match to most stellar densities, cameras, and filters.
Automated matching tolerances¶
We automatically determine the starting match tolerance (\(\delta_{tol}\)) in such a way that all patterns within each input catalog — source and reference — are clearly distinguished from each other. For each catalog independently, we find the two most similar \(N\) point patterns based on their spoke lengths. To do this, we sort the catalog by decreasing flux and create \(N\) point patterns in the same way as the main algorithm, for a total of \(n-N\) patterns where \(n\) is the number of objects in catalog. We compute the lengths of each of the \(N-1\) spokes in the pattern, and find the two patterns with the most similar spoke lengths. We then take the average spoke length difference between the two patterns. Having performed this analysis for both catalogs, we choose the smaller of the two to serve as \(\delta_{tol}\). By doing this, we limit the number of false postives caused by high object densities where patterns can be very similar due to chance alone.
Testing¶
Datasets¶
The pessimistic matcher has been tested with the following datasets, selected to span a range of stellar densities and qualities of optical distortion model.
CFHTLS
We use data from the Canada-France-Hawaii Telescope Legacy Survey (CFHTLS) observed at the Canada-France-Hawaii Telescope with MegaCam. The dat come from the W3 pointing of the Wide portion of the CFHTLS survey. We use a total number of 325 visits (start 704382) in the g and r bands, and 56 visits each in u (850245), i (705243), and z(850255) filters. This give a total of 17,700 CCD exposures to blindly match.
HiTS
We use data from the High Cadence Transient Survey (HiTS, [1]) observed on the Blanco 4m telescope with the Dark Energy Camera (DECam). We use observations in the g and r bands and a total of 183 visits starting with visit id 0406285 for a total of 10,980 CCDs exposures.
Hyper Suprime-Cam
We use data that was observed on the Subaru telescope using Hyper Suprime-Cam (HSC). These observations are within the galactic plane and thus have a extremely high density of reference and source objects given their position on the sky and depth. There are a total of 39 visits contained in data labeledpointing 908. This pointing starts with visit id 3350 and contains a total number of 4056 CCD exposures.
For each of these data we use the same set of reference objects derived from the Gaia DR1 [2] dataset.
Software configuration¶
All the tests below were performed with a late December 2018 weekly of the LSST stack. Note that this means
the tests were performed before the transition to the new SkyWcs system (DM-10765)
Matching was performed within the regular match/fit cycle of AstrometryTask in the meas_astrom package.
Comparisons were made by configuring the Stack to use the default (OPMb) matcher on the same data.
Both matchers were run with their default configurations, with the exception that we modified the match tolerance \(\delta_{tol}\) for the HSC timing test to give a fairer comparison with PPMb. OPMb’s default start tolerance is \(3\) arcseconds which causes the code to exit with a false positive match almost instantaneously. We instead set the tolerance to \(1\) arcseconds for this test and dataset to more helpfully compare the run time with similar starting tolerances between the codes.
Results¶
We present three complementary sets of results from testing:
- The fraction of CCD exposures from each dataset that found a good astrometric solution;
- Match quality, as quantified by the RMS scatter on the astromtric solution;
- Run-time performance.
Fraction of successful matches¶
In this section we compare the rate at which PPMb and OPMb are able to find acceptable matches on datasets spanning different densities of objects, data quality, and bandpass filters. For each dataset we set an upper-limit on what we consider a successful match/fit cycle based on the expected quality of the astrometric solution after a successful match. This are 0.02 for New Horizons and 0.10 for both CFHTLS and HitS. These numbers were derived from confirming successful matches by eye and noting the RMS scatter in arcseconds of the final astrometric solution.
In the results tables below:
- “N Successful” is the number of CCDs where a match has been found;
- “N Failed” is the number of CCDs where a match was not found;
- “Success rate” is the ration of “N Successful” to the total number of CCDs.
CFHTLS results¶
These data are taken at a high galactic latitude with a limited number of reference objects available. In addition, the total exposure time of these images (~200 seconds) means that roughly an equal number of sources are available to match given signal to noise and other quality cuts on the source centroid.
For the largest sample of CCDs we attempted to solve, observed primarily in the g and r bands, the performance of the two matchers is quite similar, differing only by roughly \(1%\) in the fraction of CCDs matched.
|
|||
|---|---|---|---|
| Method | N Successful | Success Rate (scatter < 0.10) | N Failed |
| PPMb | 11182 | 0.956 | 176 |
| OPMb | 11335 | 0.967 | 108 |
The same results hold for the 3 remaining bandpasses with both matchers performing to within \(1%\) of each other PPMb out performs OPMb in the u-band slightly though like the other two bands this difference is not significant given the absolute difference in the number of successful matches. Overall, PPMb and OPMb are performing broadly comparably on this dataset.
|
|||
|---|---|---|---|
| Method | N Successful | Success Rate (scatter < 0.10) | N Failed |
| PPMb | 1957 | 0.971 | 13 |
| OPMb | 1943 | 0.964 | 19 |
|
|||
|---|---|---|---|
| Method | N Successful | Success Rate (scatter < 0.10) | N Failed |
| PPMb | 1932 | 0.958 | 12 |
| OPMb | 1959 | 0.972 | 8 |
|
|||
|---|---|---|---|
| Method | N Successful | Success Rate (scatter < 0.10) | N Failed |
| PPMb | 1973 | 0.979 | 9 |
| OPMb | 1994 | 0.989 | 7 |
HiTS results¶
For the HiTS data, PPMb outperforms OPMb significantly, with the OPMb algorithm as implemented failing to find matches for a larger fraction of the CCD-exposures and more low quality matches (scatter > 0.10) than PPMb.
|
|||
|---|---|---|---|
| Method | N Successful | Success Rate (scatter < 0.10) | N Failed |
| PPMb | 10213 | 0.930 | 640 |
| OPMb | 8979 | 0.818 | 1724 |
New Horizons results¶
The New Horizons (NH) data presents the largest challenge for both algorithms. The data is observed within the Galactic plane and contains a high density of both reference objects and detected sources. Complicating the matching further, many of the brightest reference objects are saturated making them ill-suited for use in matching.
The density of objects in this field causes OPMb to perform very poorly. The “optimistic” nature of the algorithm causes it to exit after finding a false positive match which is easy for the algorithm to find given the density of reference objects. This is demonstrated by the low number of failed matches but the very high scatter of these matches — greater than \(1\) arcsec. PPMb avoids these false positives by forcing the algorithm to find three patterns that agree on their shift and rotation before exiting and returning matches.
| HSC (pointing=908), 4056 CCDs Median N Reference per CCD: 5442 | |||
|---|---|---|---|
| Method | N Successful | Success Rate (scatter < 0.10) | N Failed |
| PPMb | 3863 | 0.952 | 10 |
| OPMb | 464 | 0.114 | 0 |
Match quality comparisons¶
In addition to the looking at the fraction of successfully matched CCDs, we also examine at the quality of those matches and the astrometric solutions they produce
First we present the results for all CCDs that were successfully matched and solved by the two algorithms. For the New Horizons sample, we see that the solutions produced by OPMb are of poor quality: their RMS scatter on the solution is greater than several times the pixel scale (\(\sim 0.16\) arcseconds). PPMb fares better, although some solutions still have a large RMS scatter and pull both the mean and variance to higher values.
For HiTS and CFHTLS the two algorithms are more comparable with PPMb having a slightly wider distribution around the average solution.
| All solved CCDs | ||||
|---|---|---|---|---|
| N Matched | Mean Scatter [arcsec] | Median Scatter [arcsec] | Sigma Scatter [arcsec] | |
| HSC: PPMb | 4046 | 0.020 | 0.008 | 0.088 |
| HSC: OPMb | 4056 | 1.183 | 1.2860 | 0.4452 |
| HiTS: PPMb | 10340 | 0.016 | 0.014 | 0.035 |
| HiTS: OPMb | 9256 | 0.011 | 0.011 | 0.005 |
| CFHTLS: PPMb | 11524 | 0.065 | 0.061 | 0.159 |
| CFHTLS: OPMb | 11592 | 0.064 | 0.062 | 0.036 |
The following table shows the summary statistics computed on the same data as above but now \(5 \sigma\) clipped around the mean to compare the results with outliers removed.
| 5 Sigma clipped | ||||
|---|---|---|---|---|
| N Matched | Mean Scatter [arcsec] | Median Scatter [arcsec] | Sigma Scatter [arcsec] | |
| HSC: PPMb | 3850 | 0.008 | 0.008 | 0.001 |
| HSC: OPMb | 4052 | 1.184 | 1.286 | 0.444 |
| HiTS: PPMb | 10126 | 0.015 | 0.014 | 0.005 |
| HiTS: OPMb | 8965 | 0.011 | 0.011 | 0.004 |
| CFHTLS: PPMb | 11233 | 0.061 | 0.061 | 0.012 |
| CFHTLS: OPMb | 11531 | 0.063 | 0.062 | 0.015 |
Run-time tests¶
One concern with the generalizations added to OPMb to make PPMb is if the algorithm can still find matches in
running time comparable to that of the current Stack implementation of OPMb. In this section we present timing
results both for a field with low density and with a high density. We count the time spent matching from the
moment the doMatches is called until an array of matches (even if it is empty) is returned. We run through
all CCDs in the CFHTLS in the g, r sample run previously and all of the CCD-exposures in NH pointing 908. For
both methods there are outliers that heavily skew the mean and variance and thus we clip the times with a
\(5 \sigma\) iterative clipping.
| Method Timing Comparison (5 sigma clipped) | |||
|---|---|---|---|
| Mean time [seconds] | Median time [seconds] | Sigma time [seconds] | |
| HSC: PPMb | 86.126 | 15.996 | 112.800 |
| HSC: OPMb | 68.690 | 12.347 | 123.853 |
| CFHTLS: PPMb | 0.616 | 0.566 | 0.239 |
| CFHTLS: OPMb | 0.516 | 0.498 | 0.150 |
Both the mean and the median figures above suggest that PPMb is between 10% and 30% slower than OPMb for these datasets. However, it should be noted that PPMb is currently implemented in pure Python using NumPy. The main pattern creation loop of PPMb relies mostly on internal Python iteration which can be very slow. This is in comparison the Stack implementation of OPMb which is coded in C++. The extra steps of PPMb then do not catastrophically increase the compute time to find astrometric matches.
Summary¶
In this technical note, we have described a generalization to the OPMb algorithm from [3] that allows for astrometric matching of catalog of detected sources into a catalog of reference objects in tractable time for a larger dynamic range of object densities. Such a generalization is important for the denser galactic pointings of the LSST survey. We have shown that the PPMb algorithm to perform similarly both in terms of match success rate and WCS scatter to that of OPMb in data with a low object density, and that it provides a substantial improvement in fields with high object density. The run-time performance of the two algorithms is surprisingly comparable given that the current Stack implementation of OPMb is written in a compiled language where as PPMb is pure Python. Given the performance comparison between the two algorithms and codes, we conclude that one could switch the default behavior of the LSST Stack to PPMb without any notable drawbacks.
| [1] | F. Förster, J. C. Maureira, J. San Mart\’ın, M. Hamuy, J. Mart\’ınez, P. Huijse, G. Cabrera, L. Galbany, T. de Jaeger, S. González\ndash Gaitán, J. P. Anderson, H. Kunkarayakti, G. Pignata, F. Bufano, J. Litt\’ın, F. Olivares, G. Medina, R. C. Smith, A. K. Vivas, P. A. Estévez, R. Muñoz, and E. Vera. The High Cadence Transient Survey (HITS). I. Survey Design and Supernova Shock Breakout Constraints. \apj , 832:155, December 2016. arXiv:1609.03567, doi:10.3847/0004-637X/832/2/155. |
| [2] | Gaia Collaboration, A. G. A. Brown, A. Vallenari, T. Prusti, J. H. J. de Bruijne, F. Mignard, R. Drimmel, C. Babusiaux, C. A. L. Bailer-Jones, U. Bastian, and et al. Gaia Data Release 1. Summary of the astrometric, photometric, and survey properties. \aap , 595:A2, November 2016. arXiv:1609.04172, doi:10.1051/0004-6361/201629512. |
| [3] | (1, 2, 3, 4, 5) V. Tabur. Fast Algorithms for Matching CCD Images to a Stellar Catalogue. \pasa , 24:189–198, December 2007. arXiv:0710.3618, doi:10.1071/AS07028. |